Pipeline(steps=[('preprocessor',
ColumnTransformer(transformers=[('num',
Pipeline(steps=[('encoder',
MinMaxScaler()),
('imputer',
IterativeImputer(add_indicator=True,
estimator=KNeighborsRegressor(),
max_iter=20,
n_nearest_features=1,
random_state=42))]),
['Age', 'Height', 'Weight',
'FCVC', 'NCP', 'CH2O', 'FAF',
'TUE']),
('cat',
Pipeline(steps=[('ordinal_encode',
Ordi...
Pipeline(steps=[('imputer',
IterativeImputer(add_indicator=True,
estimator=KNeighborsRegressor(),
initial_strategy='most_frequent',
max_iter=20,
n_nearest_features=1,
random_state=42))])),
('encoder',
OneHotEncoder(drop='first',
handle_unknown='ignore'))]),
['Gender', 'FHO', 'FAVC',
'CAEC', 'SMOKE', 'SCC',
'CALC', 'MTRANS'])])),
('classifier', LogisticRegression(max_iter=2000))])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

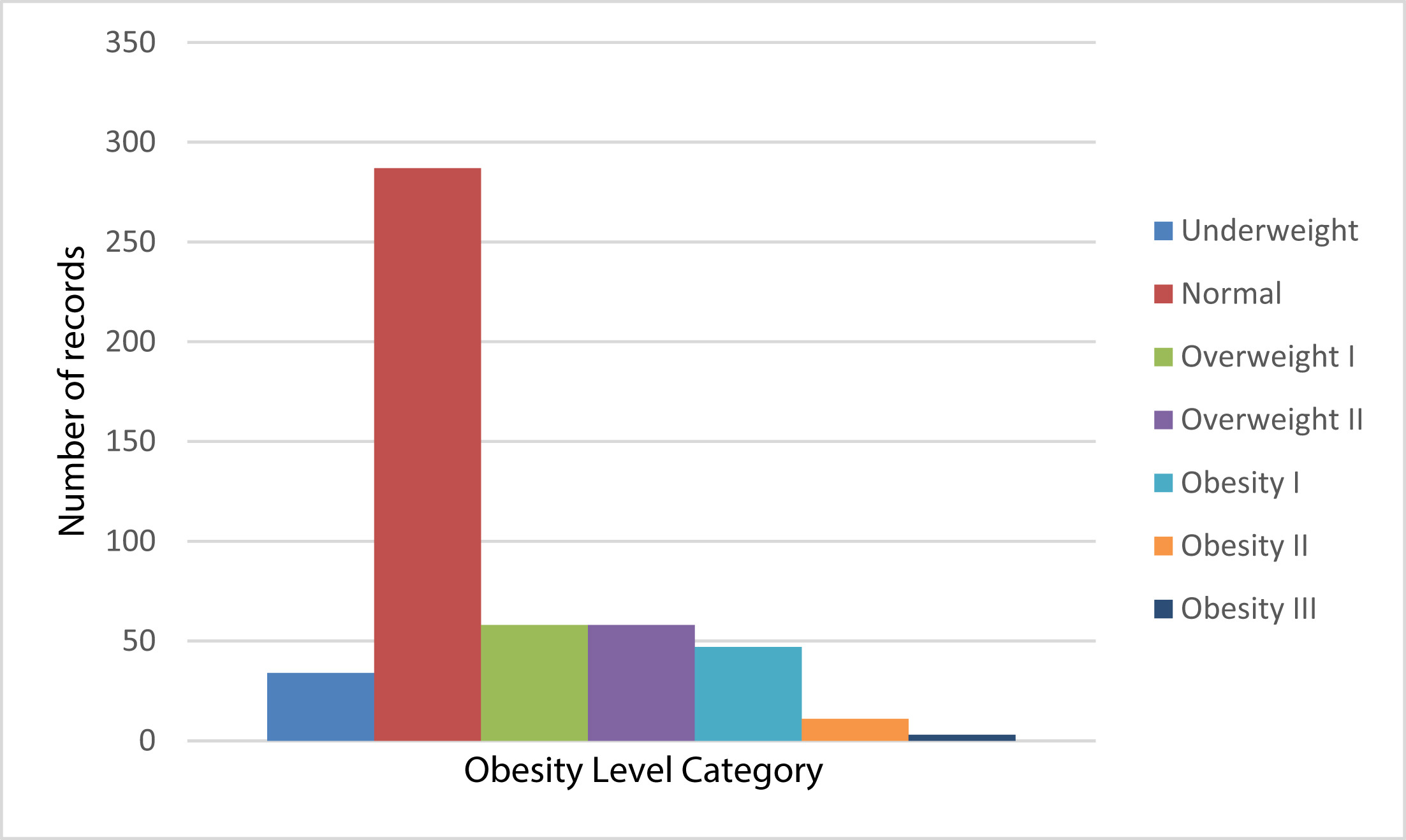 Fig 1: Original unbalanced distribution [1]
Fig 1: Original unbalanced distribution [1]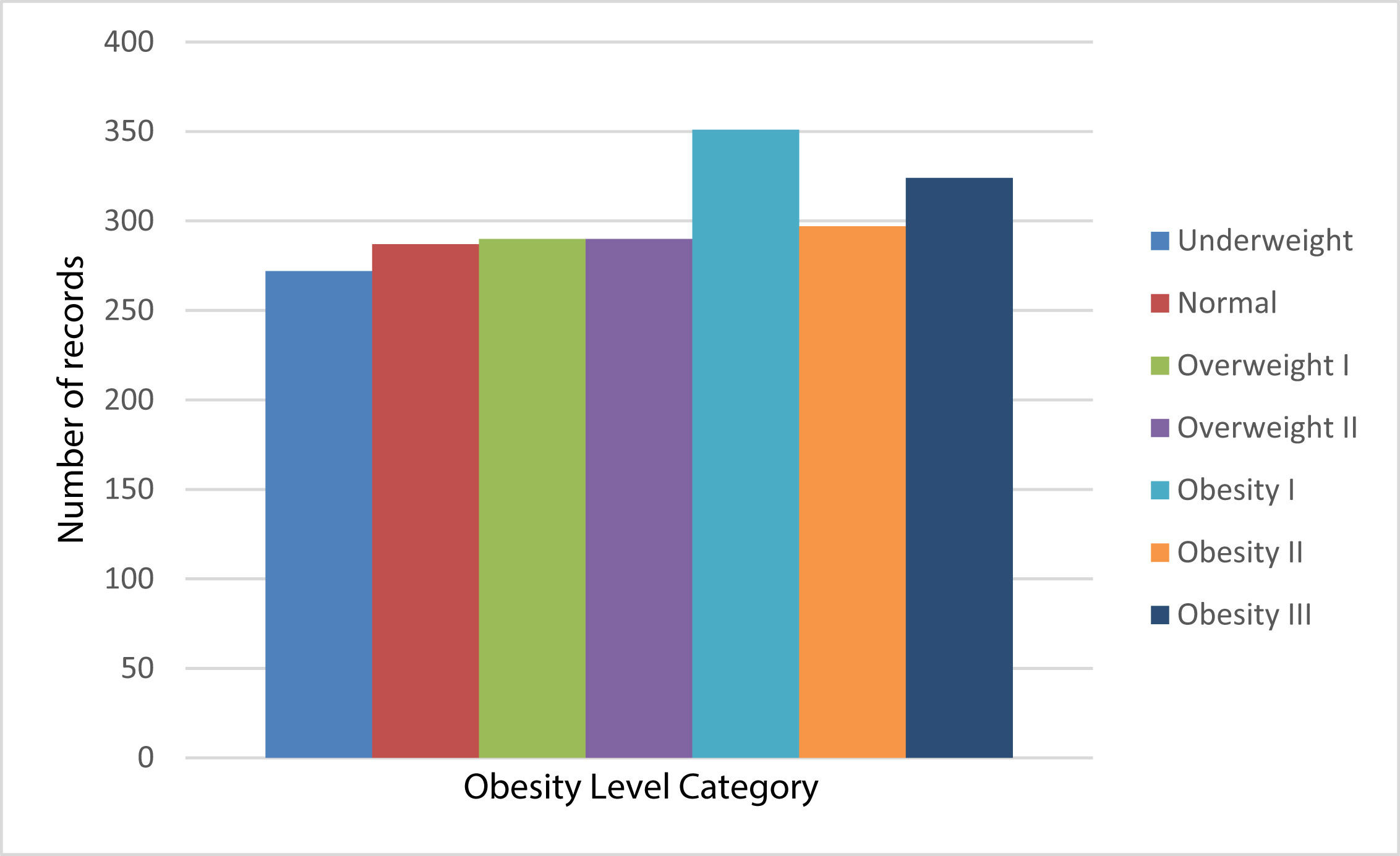 Fig 2: Oversampled balanced distribution [1]
Fig 2: Oversampled balanced distribution [1]